Chapter 10 Categorical data analysis
Now that we’ve got the basic theory behind hypothesis testing, it’s time to start looking at specific tests commonly used in psychology. We’ll start with “ tests” (pronounced as ‘chi square’) in this chapter and “-tests” (Chapter 11) in the next one. Both of these tools are very frequently used in scientific practice for comparing groups. While they’re not as powerful as “analysis of variance” (Chapter 12) and “regression” (Chapter 14), they’re much easier to understand.
The term “categorical data” is the term preferred by data analysis people, but it’s just another name for “nominal scale data”. To refresh your memory on data types, please revisit our introductory chapter on scales of measurement and types of variables (see Chapter 2.2).
In any case, categorical data analysis refers to a collection of tools that you can use when your data are nominal scale. We can use many tools for categorical data analysis, but this chapter covers the ones used by CogStat along some more common ones.
10.1 The goodness-of-fit test
The goodness-of-fit test is one of the oldest hypothesis tests around: it was invented by Karl Pearson around the turn of the century (Pearson, 1900), with some corrections made later by Sir Ronald Fisher (Fisher, 1922a). Let’s start with some psychology to introduce the statistical problem it addresses.
Over the years, there have been a lot of studies showing that humans have a lot of difficulties in simulating randomness. Try as we might to “act” random, we think in terms of patterns and structure, and so when asked to “do something at random”, what people do is anything but random. Consequently, the study of human randomness (or non-randomness, as the case may be) opens up a lot of deep psychological questions about how we think about the world. With this in mind, let’s consider a very simple study. Suppose we asked people to imagine a shuffled deck of cards and mentally pick one card from this imaginary deck “at random”. After they’ve chosen one card, we ask them to select a second one mentally. For both choices, we’re going to look at the suit (hearts, clubs, spades or diamonds) that people chose. After asking, say, people to do this, we’d like to look at the data and figure out whether or not the cards that people pretended to select were random. The data are contained in the cards.csv file, which we will load into CogStat. For the moment, let’s just focus on the first choice that people made (choice_1).
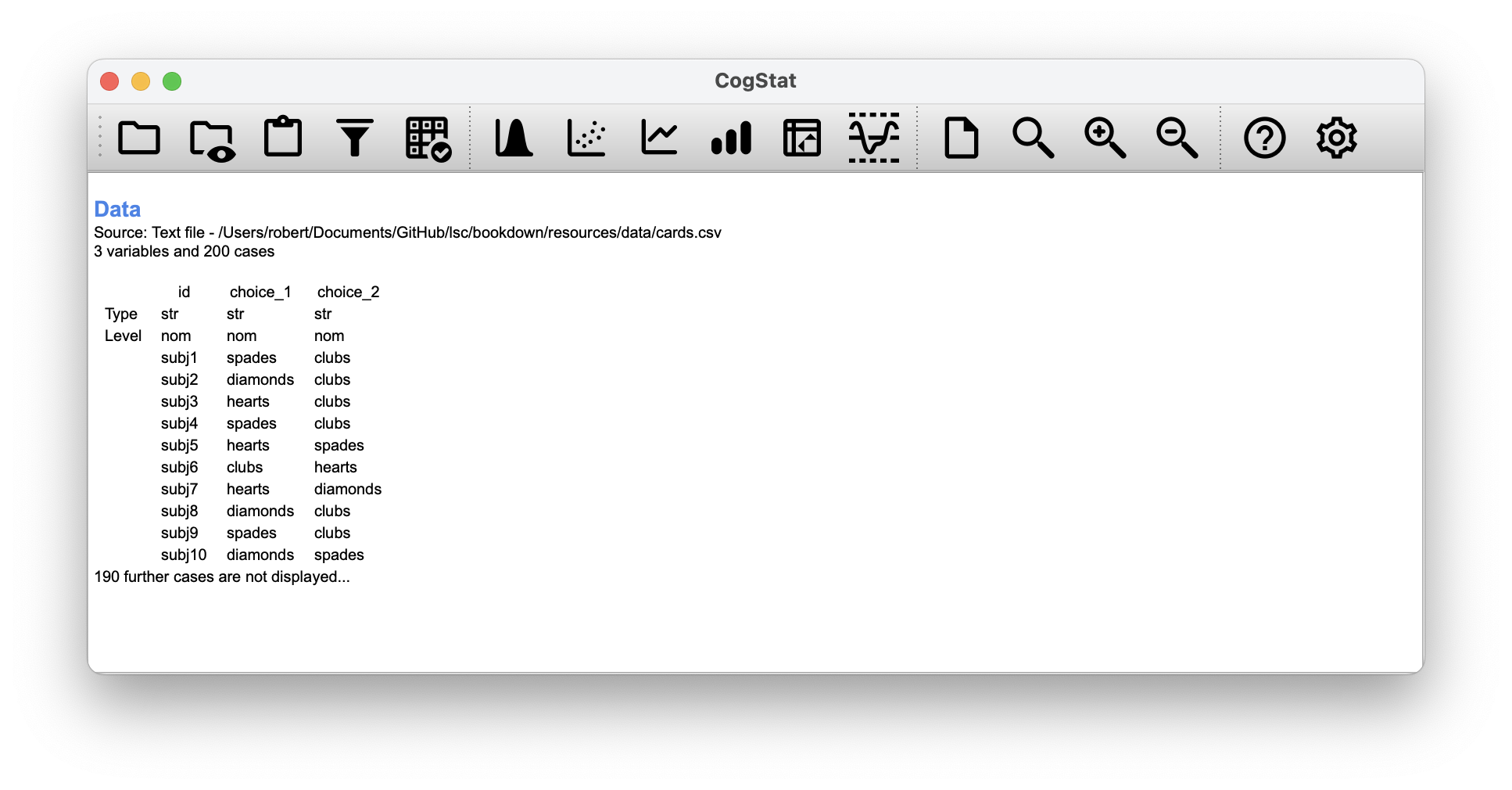
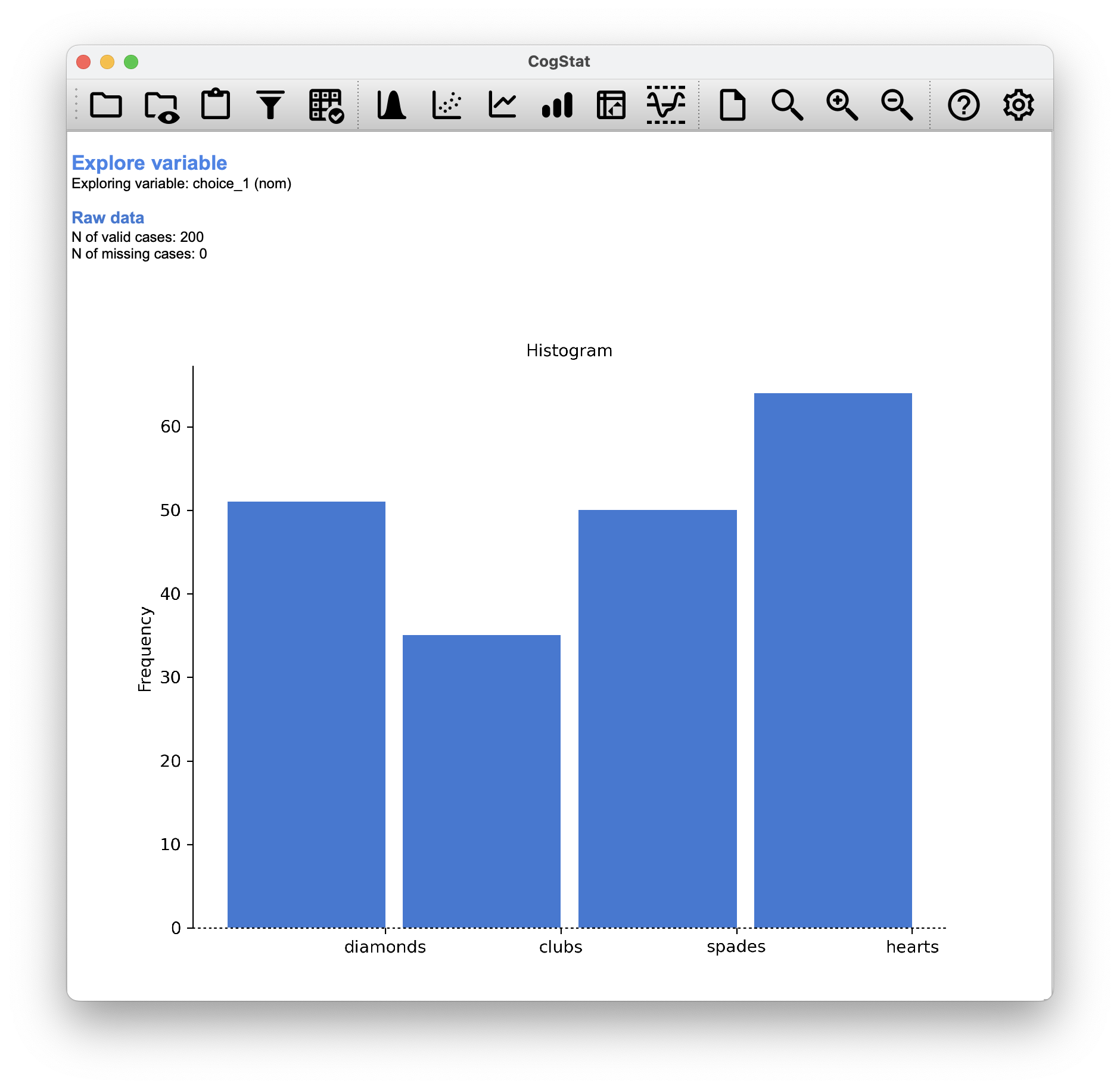
Figure 10.1: Loading the cards.csv data and running Explore variable command on choice_1
Important note: CogStat currently doesn’t support single-variable hypothesis testing for nominal scale data. However, this chapter will still be useful for you to understand the tools used in hypothesis testing, and you can use them as described here in other software packages.
We can see that the data are nominal scale, so we’ll use the goodness-of-fit test to analyze them. We’ll also use the “Fisher’s exact test” option, which is a more powerful version of the test that is appropriate when the sample size is small (less than 40). We’ll also use the “Bonferroni correction” option, which is a way of correcting for multiple comparisons. For now, let’s just run the analysis.
That little frequency table in Figure 10.1 is quite helpful. Looking at it, there’s a bit of a hint that people might be more likely to select hearts than clubs, but it’s not completely obvious just from looking at it whether that’s really true, or if this is just due to chance. So we’ll probably have to do some kind of statistical analysis to find out, which is what we’re going to talk about in the next section.
A quick side-note here: the mathematical notation of observations (i.e. an element in the data set) is , where stands for observation (but could very well be the traditional or etc.) and is the index of the observation. So is the first observation, is the second observation, and so on.
10.1.1 The null hypothesis and the alternative hypothesis
Our research hypothesis is that “people don’t choose cards randomly”. What we’re going to want to do now is translate this into some statistical hypotheses, and construct a statistical test of those hypotheses. The test is Pearson’s goodness of fit test.
As is so often the case, we have to begin by carefully constructing our null hypothesis. In this case, it’s pretty easy. First, let’s state the null hypothesis in words.
Null hypothesis (): All four suits are chosen with equal probability.
Now, because this is statistics, we have to be able to say the same thing mathematically. Let’s use the notation to refer to the true probability that the -th suit is chosen. If the null hypothesis is true, then each of the four suits has a 25% chance of being selected: in other words, our null hypothesis claims that , , and finally that . We can use to refer to the probabilities corresponding to our null hypothesis. So if we let the vector refer to the collection of probabilities that describe our null hypothesis, then we have
If the experimental task were for people to imagine they were drawing from a deck that had twice as many clubs as any other suit, then the null hypothesis would correspond to something like . As long as the probabilities are all positive numbers, and they all sum to 1, then it’s a perfectly legitimate choice for the null hypothesis. However, the most common use of the goodness of fit test is to test a null hypothesis that all categories are equally likely, so we’ll stick to that for our example.
What about our alternative hypothesis, ? We’re interested in demonstrating that the probabilities involved aren’t all identical (that is, people’s choices weren’t entirely random). As a consequence, the “human-friendly” versions of our hypotheses look like this:
Null hypothesis (): All four suits are chosen with equal probability.
Alternative hypothesis (): At least one of the suit-choice probabilities isn’t 0.25.
and the “mathematician friendly” version is
10.1.2 The “goodness of fit” test statistic
What we now want to do is construct a test of the null hypothesis. As always, if we want to test against , we will need a test statistic. The basic trick that a goodness of fit test uses is to construct a test statistic that measures how “close” the data are to the null hypothesis. If the data don’t resemble what you’d “expect” to see if the null hypothesis were true, then it probably isn’t true.
So, what would we expect to see if the null hypothesis were true? Or, to use the correct terminology, what are the expected frequencies?
There are observations, and (if the null is true) the probability of any one of them choosing a heart is , so we’re expecting hearts, right? Or, more specifically, if we let refer to “the number of category responses that we’re expecting if the null is true”, then
Clearly, what we want to do is compare the expected number of observations in each category () with the observed number of observations in that category (). And on the basis of this comparison, we ought to be able to come up with a good test statistic. To start with, let’s calculate the difference between what the null hypothesis expected us to find and what we actually did find. That is, we calculate the “observed minus expected” difference score, . This is illustrated in the following table.
| Expected frequency | 50 | 50 | 50 | 50 | |
| Observed frequency | 35 | 51 | 64 | 50 | |
| Difference score | -15 | 1 | 14 | 0 |
It’s clear that people chose more hearts and fewer clubs than the null hypothesis predicted. However, a moment’s thought suggests that these raw differences aren’t quite what we’re looking for. Intuitively, it feels like it’s just as bad when the null hypothesis predicts too few observations (which is what happened with hearts) as it is when it predicts too many (which is what happened with clubs). So it’s a bit weird that we have a negative number for clubs and a positive number for hearts.
One easy way to fix this is to square everything so that we now calculate the squared differences, .
| Expected frequency | 50 | 50 | 50 | 50 | |
| Observed frequency | 35 | 51 | 64 | 50 | |
| Difference score | -15 | 1 | 14 | 0 | |
| Squared differences | 225 | 1 | 196 | 0 |
Now we’re making progress. Now, we’ve got a collection of numbers that are big whenever the null hypothesis makes a lousy prediction (clubs and hearts) but small whenever it makes a good one (diamonds and spades).
Next, let’s also divide all these numbers by the expected frequency , so we’re calculating . Since for all categories in our example, it’s not a very interesting calculation, but let’s do it anyway.
| Expected frequency | 50 | 50 | 50 | 50 | |
| Observed frequency | 35 | 51 | 64 | 50 | |
| Difference score | -15 | 1 | 14 | 0 | |
| Squared differences | 225 | 1 | 196 | 0 | |
| Squared differences divided by expected frequency | 4.5 | 0.02 | 3.92 | 0 |
In effect, what we’ve got here are four different “error” scores, each one telling us how big a “mistake” the null hypothesis made when we tried to use it to predict our observed frequencies. So, in order to convert this into a useful test statistic, one thing we could do is just add these numbers up. We get
The result is called the goodness of fit statistic, conventionally referred to either as or GOF. If we let refer to the total number of categories (i.e. for our cards data), then the statistic is given by the following formula:
Intuitively, it’s clear that if is small, then the observed data are very close to what the null hypothesis predicted , so we’re going to need a large statistic in order to reject the null. As we’ve seen from our calculations, we’ve got a value of in our cards data set. So now the question becomes, is this a big enough value to reject the null?
10.1.3 The sampling distribution of the GOF statistic (advanced)
To determine whether or not a particular value of is large enough to justify rejecting the null hypothesis, we will need to figure out what the sampling distribution for would be if the null hypothesis were true. If you want to cut to the chase and are willing to take it on faith that the sampling distribution is a chi-squared () distribution with degrees of freedom, you can skip the rest of this section. However, if you want to understand why the goodness of fit test works the way it does, read on.
Let’s suppose that the null hypothesis is true. If so, then the true probability that an observation falls in the -th category is . After all, that’s the definition of our null hypothesis. If you think about it, this is kind of like saying that “nature” decides whether or not the observation ends up in category by flipping a weighted coin (i.e. one where the probability of getting a head is ). And therefore, we can think of our observed frequency by imagining that nature flipped of these coins (one for each observation in the data set). And exactly of them came up heads. Obviously, this is a pretty weird way to think about the experiment. But it reminds you that we’ve seen this scenario before. It’s exactly the same set-up that gave rise to the binomial distribution in Chapter 7.4.1. In other words, if the null hypothesis is true, then it follows that our observed frequencies were generated by sampling from a binomial distribution: Now, if you remember from our discussion of the central limit theorem (Section 8.3.3), the binomial distribution starts to look pretty much identical to the normal distribution, especially when is large and when isn’t too close to 0 or 1.
In other words, as long as is large enough – or, to put it another way, when the expected frequency is large enough – the theoretical distribution of is approximately normal. Better yet, if is normally distributed, then so is … since is a fixed value, subtracting off and dividing by changes the mean and standard deviation of the normal distribution.
Okay, so now let’s have a look at what our goodness of fit statistic actually is. What we’re doing is taking a bunch of things that are normally distributed, squaring them, and adding them up. As we discussed in Chapter 7.4.4, when you take a bunch of things that have a standard normal distribution (i.e. mean 0 and standard deviation 1), square them, then add them up, then the resulting quantity has a chi-square distribution. So now we know that the null hypothesis predicts that the sampling distribution of the goodness of fit statistic is a chi-square distribution.
There’s one last detail to talk about, namely the degrees of freedom. If you remember back to Chapter 7.4.4, if the number of things you’re adding up is , then the degrees of freedom for the resulting chi-square distribution is . Yet, at the start of this section, we said that the actual degrees of freedom for the chi-square goodness of fit test is . What’s up with that? The answer here is that what we’re supposed to be looking at is the number of genuinely independent things that are getting added together. And, even though there are things that we’re adding, only of them are truly independent; and so the degrees of freedom are actually only .
10.1.4 Degrees of freedom
Figure 10.2: Chi-square distributions with different values for the “degrees of freedom”.
When discussing the chi-square distribution in Chapter 7.4.4, we didn’t elaborate on what “degrees of freedom” actually mean. Looking at Figure 10.2, you can see that if we change the degrees of freedom, then the chi-square distribution changes shape substantially. But what exactly is it? It’s the number of “normally distributed variables” that we are squaring and adding together. But, for most people, that’s kind of abstract and not entirely helpful. What we really need to do is try to understand degrees of freedom in terms of our data. So here goes.
The basic idea behind degrees of freedom is quite simple: you calculate it by counting up the number of distinct “quantities” that are used to describe your data; and then subtracting off all of the “constraints” that those data must satisfy.40 This is a bit vague, so let’s use our cards.csv data as a concrete example.
We describe our data using four numbers, , , and corresponding to the observed frequencies of the four different categories (hearts, clubs, diamonds, spades). These four numbers are the random outcomes of our experiment. But, the experiment has a fixed constraint built into it: the sample size .41 That is, if we know how many people chose hearts, how many chose diamonds and how many chose clubs, then we’d be able to figure out exactly how many chose spades. In other words, although our data are described using four numbers, they only actually correspond to degrees of freedom. A slightly different way of thinking about it is to notice that there are four probabilities that we’re interested in (again, corresponding to the four different categories), but these probabilities must sum to one, which imposes a constraint. Therefore, the degrees of freedom is . Regardless of whether you want to think about it in terms of the observed frequencies or in terms of the probabilities, the answer is the same. In general, when running the chi-square goodness of fit test for an experiment involving groups, then the degrees of freedom will be .
10.1.5 Testing the null hypothesis
Figure 10.3: Illustration of how the hypothesis testing works for the chi-square goodness of fit test.
The final step in constructing our hypothesis test is to figure out what the rejection region is. That is, what values of would lead us to reject the null hypothesis? As we saw earlier, large values of imply that the null hypothesis has done a poor job of predicting the data from our experiment, whereas small values of imply that it’s actually done pretty well. Therefore, a pretty sensible strategy would be to say there is some critical value, such that if is bigger than the critical value, we reject the null; but if is smaller than this value, we retain the null.
In other words, to use the language we introduced in Chapter 9, the chi-squared goodness of fit test is always a one-sided test. If we want our test to have a significance level of (that is, we are willing to tolerate a Type I error rate of 5%), then we have to choose our critical value so that there is only a 5% chance that could get to be that big if the null hypothesis is true. Meaning that we want the 95th percentile of the sampling distribution. This is illustrated in Figure 10.3. So if our statistic is bigger than 7.814728, then we can reject the null hypothesis. Since we calculated that before (i.e. ), we can reject the null.
The corresponding -value is 0.03774185. This is the probability of getting a value of as big as 8.44, or bigger, if the null hypothesis is true. Since this is less than our significance level of , we can reject the null hypothesis.
And that’s it, basically. You now know Pearson’s test for the goodness of fit.
10.1.6 How to report the results of the test
If we wanted to write this result up for a paper or something, the conventional way to report this would be to write something like this:
Of the 200 participants in the experiment, 64 selected hearts for their first choice, 51 selected diamonds, 50 selected spades, and 35 selected clubs. A chi-square goodness of fit test was conducted to test whether the choice probabilities were identical for all four suits. The results were significant (), suggesting that people did not select suits purely at random.
This is pretty straightforward, and hopefully it seems pretty unremarkable. There are a few things that you should note about this description:
- The statistical test is preceded by descriptive statistics. That is, we told the reader something about what the data looked like before going on to do the test. In general, this is good practice: remember that your reader doesn’t know your data anywhere near as well as you do. So unless you describe it to them adequately, the statistical tests won’t make sense to them.
- The description tells you what the null hypothesis being tested is. Writers don’t always do this, but it’s often a good idea in those situations where some ambiguity exists; or when you can’t rely on your readership being intimately familiar with the statistical tools you’re using. Quite often, the reader might not know (or remember) all the details of the test that your using, so it’s a kind of politeness to “remind” them! As far as the goodness of fit test goes, you can usually rely on a scientific audience knowing how it works (since it’s covered in most intro stats classes). However, it’s still a good idea to explicitly state the null hypothesis (briefly!) because the null hypothesis can differ depending on your test. For instance, in the cards example our null hypothesis was that all the four suit probabilities were identical (i.e. ), but there’s nothing special about that hypothesis. We could just as easily have tested the null hypothesis that and using a goodness of fit test. So it’s helpful to the reader to explain your null hypothesis to them. Also, we described the null hypothesis in words, not in maths. That’s perfectly acceptable. You can describe it in maths if you like, but since most readers find words easier to read than symbols, most writers tend to describe the null using words if they can.
- A “stat block” is included. When reporting the results of the test itself, we didn’t just say that the result was significant; we included a “stat block” (i.e. the dense mathematical-looking part in the parentheses), which reports all the “raw” statistical data. For the chi-square goodness of fit test, the information that gets reported is the test statistic (that the goodness of fit statistic was 8.44), the information about the distribution used in the test ( with 3 degrees of freedom, which is usually shortened to ), and then the information about whether the result was significant (in this case ). The particular information that needs to go into the stat block is different for every test, and so each time we introduce a new test, we’ll show you what the stat block should look like.
- The results are interpreted. In addition to indicating that the result was significant, we provided an interpretation of the result (i.e. that people didn’t choose randomly). This is also a kindness to the reader because it tells them what they should believe about your data. If you don’t include something like this, it’s tough for your reader to understand what’s going on.42
As with everything else, your overriding concern should be that you explain things to your reader.
10.1.7 A comment on statistical notation (advanced)
If you’ve been reading very closely, there is one thing about how we wrote up the chi-square test in the last section that might be bugging you a little bit. There’s something that feels a bit wrong with writing “”, you might be thinking. After all, it’s the goodness of fit statistic that is equal to 8.44, so shouldn’t I have written or maybe GOF? This seems to be conflating the sampling distribution (i.e. with ) with the test statistic (i.e. ). You figured it was a typo since and look pretty similar. Oddly, it’s not. Writing is essentially a highly condensed way of writing “the sampling distribution of the test statistic is , and the value of the test statistic is 8.44”.
In one sense, this is kind of stupid. There are lots of different test statistics out there that have a chi-square sampling distribution: the statistic that we’ve used for our goodness of fit test is only one of many (albeit one of the most commonly encountered ones). In a sensible, perfectly organised world, we’d always have a separate name for the test statistic and the sampling distribution: that way, the stat block itself would tell you precisely what it was that the researcher had calculated. Sometimes this happens.
For instance, the test statistic used in the Pearson goodness of fit test is written ; but there’s a closely related test known as the -test43 (Sokal & Rohlf, 1994), in which the test statistic is written as . As it happens, the Pearson goodness of fit test and the -test both test the same null hypothesis; and the sampling distribution is exactly the same (i.e. chi-square with degrees of freedom). If we’d done a -test for the cards data rather than a goodness of fit test, then we’d have ended up with a test statistic of , which is slightly different from the ; and produces a slightly smaller -value of . Suppose that the convention was to report the test statistic, then the sampling distribution, and then the -value. If that were true, then these two situations would produce different stat blocks: the original result would be written , whereas the new version using the -test would be written as . However, using the condensed reporting standard, the original result is written , and the new one is written , and so it’s actually unclear which test was actually run.
So why don’t we live in a world where the stat block’s contents uniquely specify what tests were run? Any test statistic that follows a distribution is commonly called a “chi-square statistic”; anything that follows a -distribution is called a “-statistic” and so on. But, as the versus example illustrates, two different things with the same sampling distribution are still, well, different. Consequently, it’s sometimes a good idea to be clear about what the actual test was that you ran, especially if you’re doing something unusual. If you just say “chi-square test”, it’s unclear what test you’re talking about. Although, since the two most common chi-square tests are the goodness of fit test and the independence test (Section 10.2), most readers with stats training can probably guess. Nevertheless, it’s something to be aware of.
10.2 The test of independence (or association)
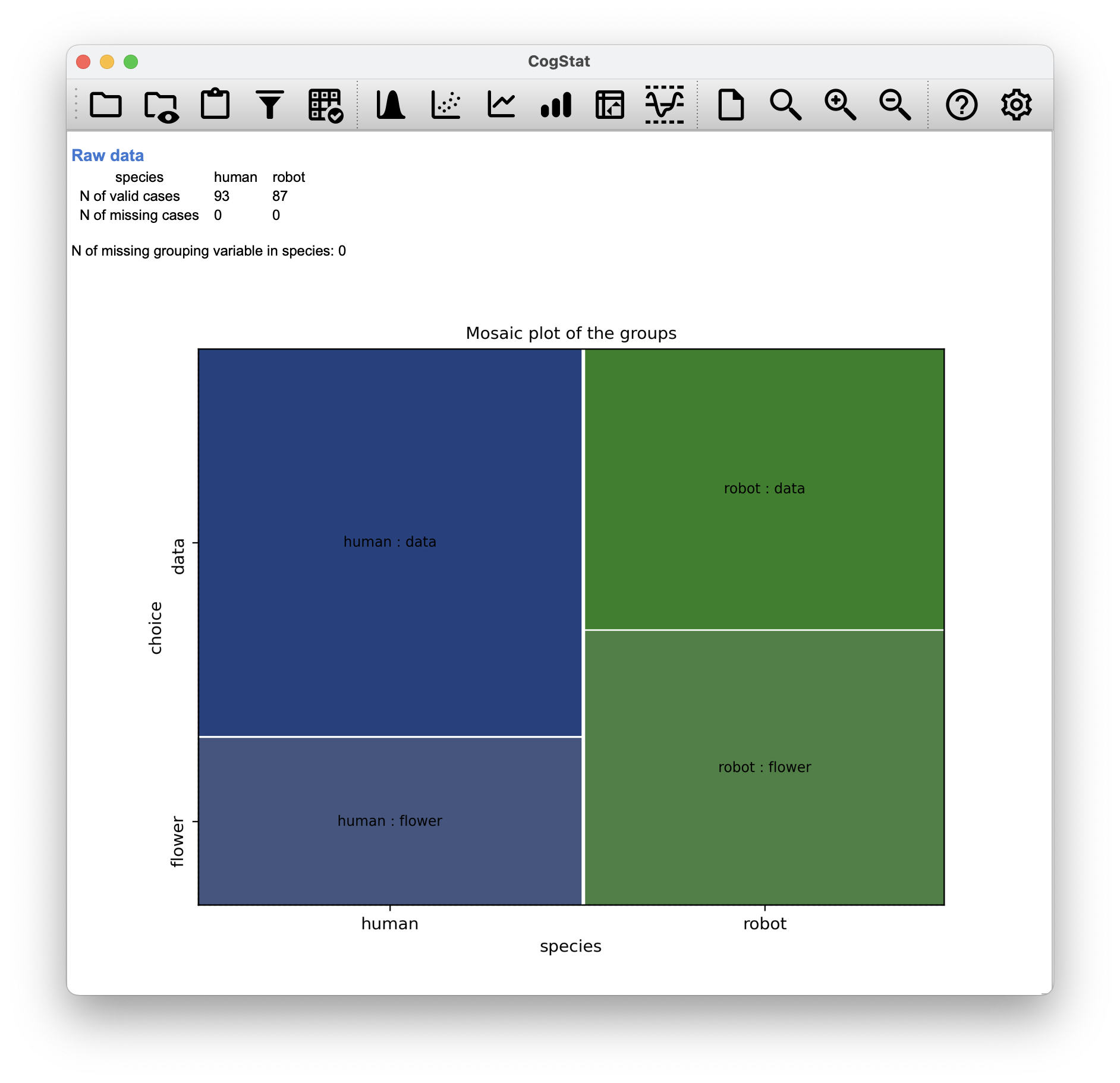
The other day Danielle was watching an animated documentary examining the quaint customs of the natives of the planet Chapek 9. Apparently, in order to gain access to their capital city, a visitor must prove that they’re a robot, not a human. In order to determine whether or not the visitor is human, they ask whether the visitor prefers puppies, flowers or large, properly formatted data files. But what if humans and robots have the same preferences? That probably wouldn’t be a very good test then, would it? In order to determine whether or not a visitor is human, the natives of Chapek 9 need to know whether or not the visitor’s preferences are independent of their species. In other words, they need to know whether or not the visitor’s preferences are associated with their species.
Figure 10.4: Loading the chapek9.csv data set into CogStat.
In total, there are 180 entries in the data frame, one for each person (counting both robots and humans as “people”) who was asked to make a choice. Specifically, there are 93 humans and 87 robots.
What we want to do is look at the choices broken down by species. That is, we need to cross-tabulate the data. We cannot use the Pivot table option in CogStat for strings, but we can use the Compare groups option instead. We’ll use the species variable as the grouping variable and the choices variable as the variable to compare.
Figure 10.5: Using the Compare groups dialogue to get some information about choices by species.
The overwhelmingly preferred choice is the data file. You can see a visual representation of this in Figure 10.6.
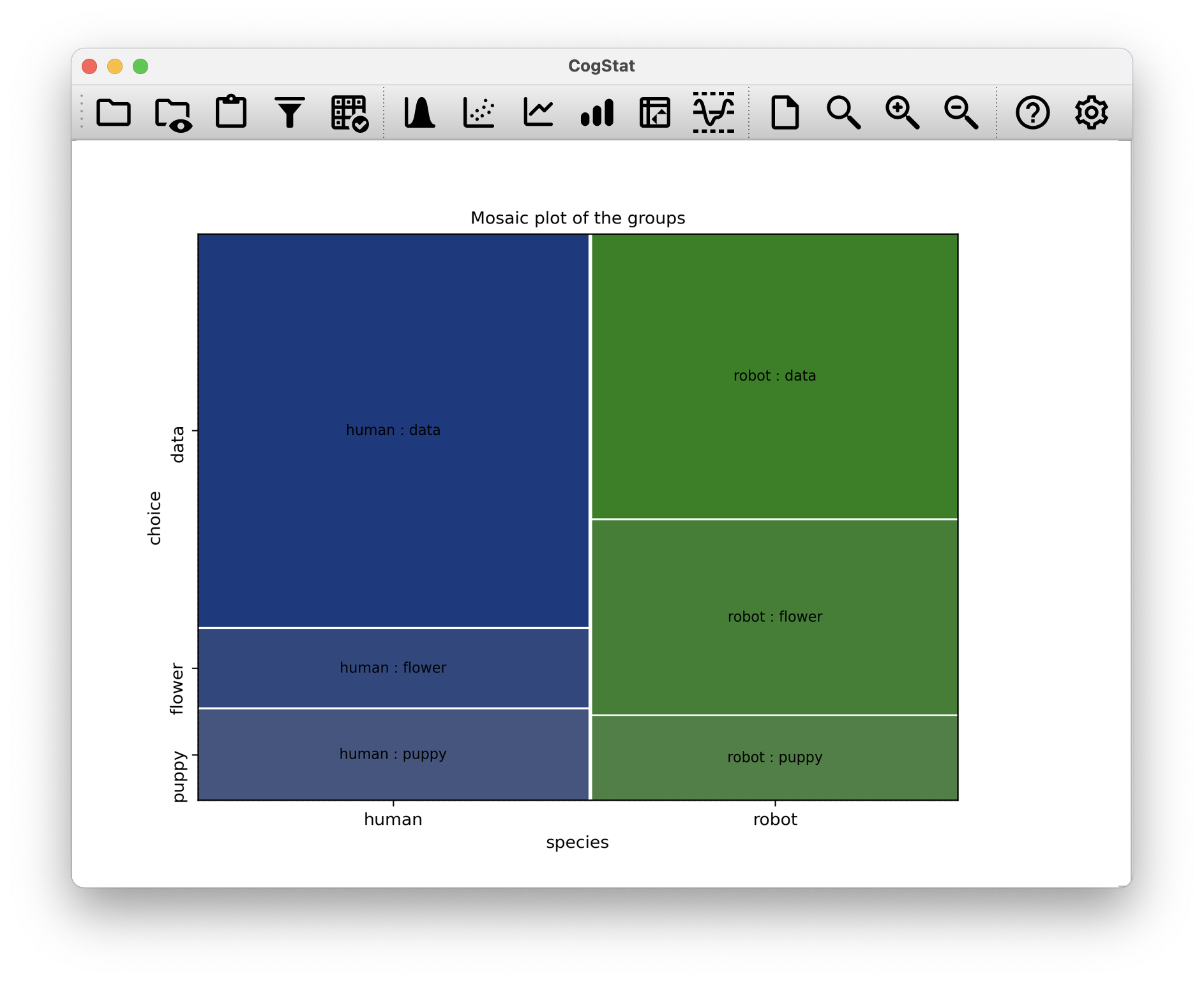
Figure 10.6: The mosaic plot of choices by species.
Scrolling down, you can see the descriptives for the groups in the Sample properties section:
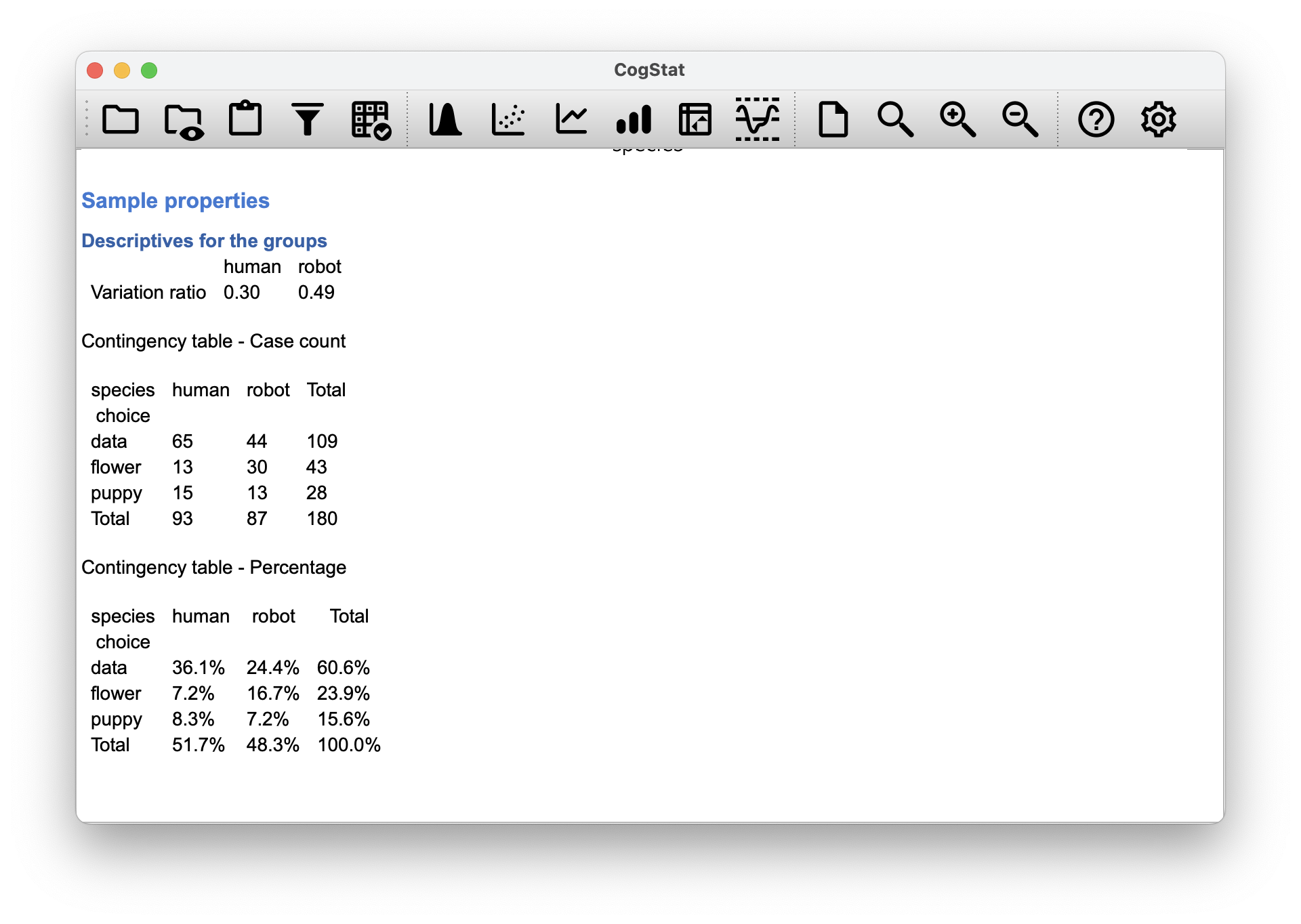
Figure 10.7: The Sample properties section of the Compare groups results showing the contingency table we’ll discuss later in this chapter.
Let’s put these results in a table for our discussion on the test of independence.
| Robot | Human | Total | |
| Puppy | 13 | 15 | 28 |
| Flower | 30 | 13 | 43 |
| Data file | 44 | 65 | 109 |
| Total | 87 | 93 | 180 |
It’s quite clear that most humans chose the data file, whereas the robots tended to be a lot more even in their preferences. Leaving aside the question of why humans might be more likely to choose the data file for the moment, first, we must determine if the discrepancy between human choices and robot choices in the data set is statistically significant.
10.2.1 Constructing our hypothesis test
How do we analyse this data manually? Specifically, since our research hypothesis is that “humans and robots answer the question in different ways”, how can we construct a test of the null hypothesis that “humans and robots answer the question the same way”? As before, we begin by establishing some notation to describe the data:
| Robot | Human | Total | |
|---|---|---|---|
| Puppy | |||
| Flower | |||
| Data file | |||
| Total |
In this notation, we say that is a count (observed frequency) of the number of respondents that are of species (robot or human) who answered (puppy, flower or data) when asked to make a choice. The total number of observations is written , as usual. Finally, denotes the row totals (e.g. is the total number of people who chose the flower), and denotes the column totals (e.g., is the total number of robots). To use the terminology from another mathematical statistics textbook (Hogg et al., 2005), we should technically refer to this situation as a chi-square test of homogeneity; and reserve the term chi-square test of independence for the situation where both the row and column totals are random outcomes of the experiment.
So now, let’s think about what the null hypothesis says. If robots and humans are responding in the same way to the question, it means that the probability that “a robot says puppy” is the same as the probability that “a human says puppy”, and so on for the other two possibilities. So, if we use to denote “the probability that a member of species gives response ”, then our null hypothesis is that:
| : | All of the following are true: | |
|---|---|---|
same probability of saying puppy |
||
same probability of saying flower |
||
same probability of saying data file |
Since the null hypothesis claims that the true choice probabilities don’t depend on the species of the person making the choice, we can let refer to this probability: e.g. is the true probability of choosing the puppy.
Next, in much the same way we did with the goodness of fit test, we need to calculate the expected frequencies. For each of the observed counts , we need to figure out what the null hypothesis would tell us to expect. Let’s denote this expected frequency by . This time, it’s a little bit trickier. If there are a total of people that belong to species , and the true probability of anyone (regardless of species) choosing option is , then the expected frequency is just:
This is all very well and good, but we have a problem. Unlike the situation we had with the goodness of fit test, the null hypothesis doesn’t specify a particular value for . It’s something we have to estimate (Chapter 8) from the data! Fortunately, this is pretty easy to do. If 28 out of 180 people selected the flowers, then a natural estimate for the probability of choosing flowers is , which is approximately . If we phrase this in mathematical terms, what we’re saying is that our estimate for the probability of choosing option is just the row total divided by the total sample size:
Therefore, our expected frequency can be written as the product (i.e. multiplication) of the row total and the column total, divided by the total number of observations:44
Now that we’ve figured out how to calculate the expected frequencies, it’s straightforward to define a test statistic following the same strategy we used in the goodness of fit test. It’s pretty much the same statistic. For a contingency table with rows and columns, the equation that defines our statistic is The only difference is that we have to include two summation signs (i.e. ) to indicate that we’re summing over both rows and columns. As before, large values of suggest that the null hypothesis provides a poor description of the data, whereas small values of indicate that it does a good job of accounting for the data. Therefore, just like last time, we want to reject the null hypothesis if is too large.
Not surprisingly, this statistic is distributed. All we need to do is figure out how many degrees of freedom are involved, which actually isn’t too hard. You can think of the degrees of freedom as equal to the number of data points you’re analysing minus the number of constraints. A contingency table with rows and columns contains a total of observed frequencies, so that’s the total number of observations.
What about the constraints? Here, it’s slightly trickier. The answer is always the same:
But the explanation for why the degrees of freedom take this value is different depending on the experimental design. For the sake of argument, let’s suppose that we had honestly intended to survey exactly 87 robots and 93 humans (column totals fixed by the experimenter) but left the row totals free to vary (row totals are random variables). Let’s think about the constraints that apply here. Well, since we deliberately fixed the column totals, we have constraints right there. There’s more to it than that. Remember how our null hypothesis had some free parameters (i.e. we had to estimate the values)? Those matter too.
Every free parameter in the null hypothesis is rather like an additional constraint. So, how many of those are there? Well, since these probabilities have to sum to 1, there’s only of these. So our total degree of freedom is:
Alternatively, suppose that the only thing that the experimenter fixed was the total sample size . That is, we quizzed the first 180 people that we saw, and it just turned out that 87 were robots and 93 were humans. This time around, our reasoning would be slightly different but would still lead us to the same answer. Our null hypothesis still has free parameters corresponding to the choice probabilities. Still, it now also has free parameters corresponding to the species probabilities because we’d also have to estimate the probability that a randomly sampled person turns out to be a robot.45 Finally, since we did fix the total number of observations , that’s one more constraint. So now we have, observations, and constraints. What does that give? Amazing.
10.2.2 The test results in CogStat
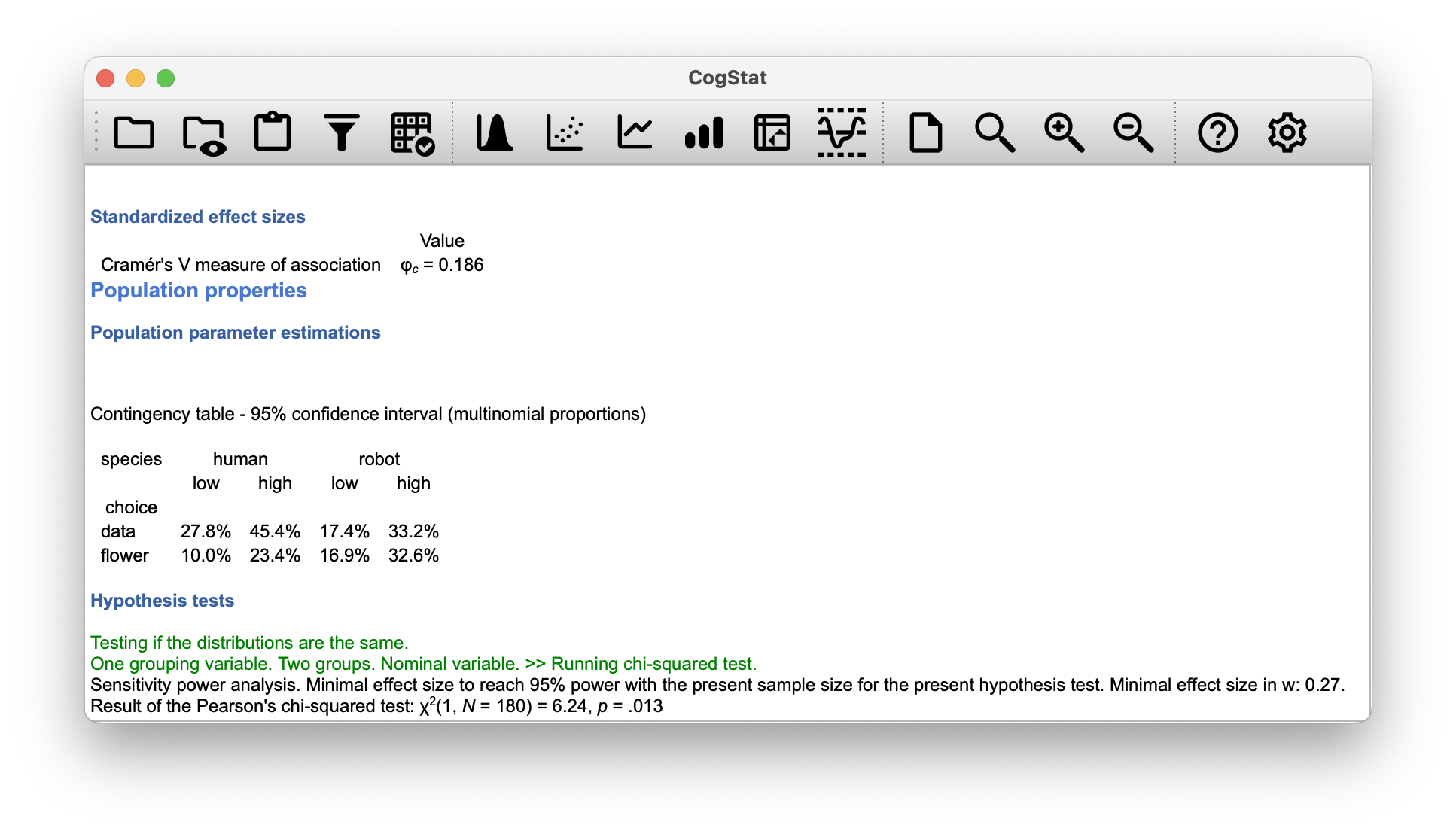
The test is automatically done in CogStat using the Compare groups feature. The result set will contain information about the sample and its properties, as seen in Figure 10.7. Further scrolling down, you’ll see the effect size (which we will cover in a short while in Chapter 10.4). The last part of the result set is the hypothesis test itself (see Figure 10.8).
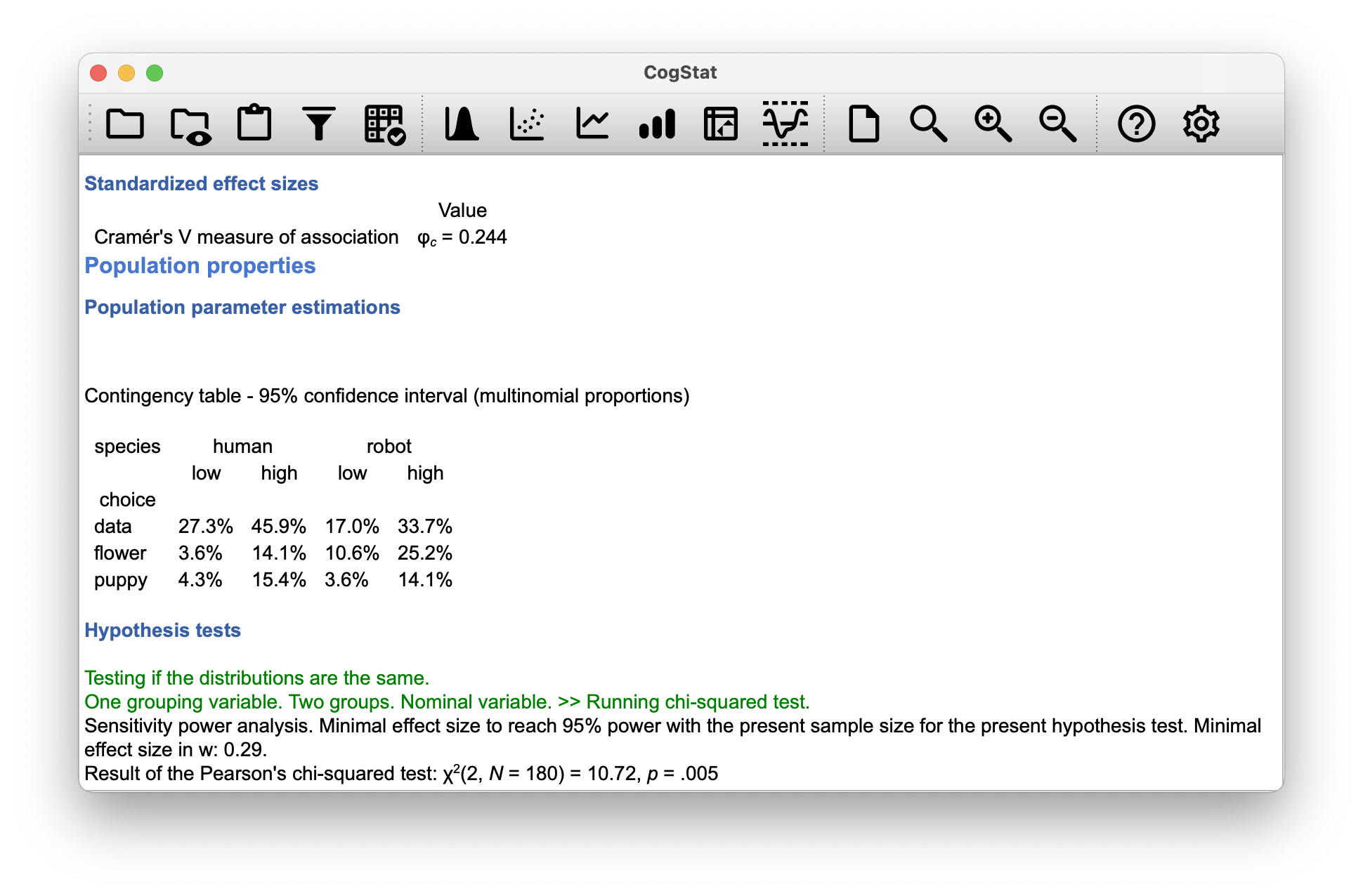
Figure 10.8: Population properties and Hypothesis tests for the chapek9.csv data set.
Let us go through the Hypothesis tests section line by line.
Hypothesis tests
Testing if the distributions are the same.
One grouping variable. Two groups. Nominal variable. >> Running chi-squared test.
Sensitivity power analysis. Minimal effect size to reach 95% power with the present sample size for the present hypothesis test. Minimal effect size in w: 0.29.
Result of the Pearson's chi-squared test: χ2(2, N = 180) = 10.72, p = .005
Testing if the distributions are the same.: This, in plain English, tells us that we are testing for a null hypothesis where all distributions of all group, or probabilities, are the same. It does not differ in essence from the we described more eloquently in Table 10.2.One grouping variable.: This says we are looking at only one variable by which we have dissected our data:species.Two groups: This tells us that we have two groups,robotandhuman.Nominal variable.: This tells us that the variable we are looking at is categorical.Running chi-squared test.: Based on all the above, CogStat has decided to run a test.
Let us ignore the details about the 95% confidence interval, minimal effect size w, and Cramér’s V (Figure 10.8) for now. We will come back to them in Chapter 10.4.
Result of the Pearson's chi-squared test:
The test result is 10.72, the degree of freedom is 2 with 180 observations, and the p-value is 0.005. This means that the null hypothesis is rejected at the 0.005 level of significance.
This output gives us enough information to write up the result:
Pearson’s revealed a significant association between species and choice (): robots appeared to be more likely to say that they prefer flowers, but the humans were more likely to say they prefer data.
Notice that, once again, we provided a little bit of interpretation to help the human reader understand what’s going on with the data. This is a good habit to get into. It’s also a good idea to report the effect size, which we will do in the next section.
10.3 Yates correction for 1 degree of freedom
Time for a little bit of a digression. You need to make a tiny change to your calculations whenever you only have 1 degree of freedom. It’s called the continuity correction, or sometimes the Yates correction.
The test is based on an approximation, specifically on the assumption that binomial distribution starts to look like a normal distribution for large . One problem with this is that it often doesn’t quite work, especially when you’ve only got 1 degree of freedom (e.g. when you’re doing a test of independence on a contingency table). The main reason for this is that the true sampling distribution for the statistic is actually discrete (because you’re dealing with categorical data!), but the distribution is continuous. This can introduce systematic problems. Specifically, when is small and when , the goodness of fit statistic tends to be “too big”, meaning that you actually have a bigger value than you think (or, equivalently, the values are a bit too small). Yates (1934) suggested a simple fix, in which you redefine the goodness of fit statistic as: Basically, he subtracts off 0.5 everywhere. The correction is basically a hack. It’s not derived from any principled theory: rather, it’s based on an examination of the behaviour of the test and observing that the corrected version seems to work better.
CogStat (and many other software, for that matter) introduces this correction, so it’s useful to know what it is about. You won’t know when it happens because the CogStat output doesn’t explicitly say that it has used a “continuity correction” or “Yates’ correction”.46
Let us overwrite all the puppy answers in our chapek9 data frame to look at 1 degree of freedom (Figure 10.9). Let’s use the chapek9two.csv data set for this.
The result as calculated by default with the Yates correction is:
However, had we not applied the Yates correction, the results would have been , which is a bit different. The difference is not huge, but it is there. The Yates correction is a good thing to know about, but it’s not something you need to worry about too much. It’s just a little bit of a hack that makes the test work better in this specific case.
10.4 Effect size (Cramér’s )
As we discussed earlier in Chapter 9.7, it’s becoming commonplace to ask researchers to report some measure of effect size. So, suppose that you’ve run your chi-square test, which turns out to be significant. So you now know that there is some association between your variables (independence test) or some deviation from the specified probabilities (goodness of fit test). Now you want to report a measure of effect size. That is, given that there is an association/deviation, how strong is it?
There are several different measures you can choose to report and several different tools you can use to calculate them. By default, the two measures that people tend to report most frequently are the (pronounced: “phi”) statistic and the somewhat superior version, known as Cramér’s . While CogStat gives you only Cramér’s , we need to start with because they are related.
Mathematically, they’re both very simple. To calculate the statistic, you just divide your value by the sample size and take the square root:
The idea here is that the statistic is supposed to range between 0 (no association at all) and 1 (perfect association). However, it doesn’t always do this when your contingency table is bigger than (like in our original chapek9 data set), which is a total pain. So, to correct this, people usually prefer to report the statistic proposed by Cramér (1946). It’s a pretty simple adjustment to . If you’ve got a contingency table with rows and columns, then define to be the smaller of the two values. If so, then Cramér’s statistic is And you’re done. This seems to be a reasonably popular measure, presumably because it’s easy to calculate, and it gives answers that aren’t completely silly: you know that does range from 0 (no association at all) to 1 (perfect association).
Calculating is automatic in CogStat, as you’ve seen in the result sets earlier in both the original chapek9 data set (Figure 10.8) and the modified one (Figure 10.9). Now let’s look at the original chapek9 effect size.
Standardized effect sizes
| Value | |
| Cramér's V measure of association | ϕc = 0.244 |
A Cramer’s V of 0.244 tells us that there is a moderate association between the two variables. The usual guidance is that anything below 0.2 is a weak association, 0.2 to 0.6 is a moderate association, and anything above 0.6 is a strong association. However, you must always look at the context of your data when determining the effect size.
10.5 Assumptions of the test(s)
All statistical tests make assumptions, and it’s usually a good idea to check that those assumptions are met. For the chi-square tests discussed so far in this chapter, the assumptions are:
- Expected frequencies are sufficiently large. Remember how in the previous section, we saw that the sampling distribution emerges because the binomial distribution is similar to a normal distribution? Well, as we discussed in Chapter 7, this is only true when the number of observations is sufficiently large. What that means in practice is that all of the expected frequencies need to be reasonably big. How big is reasonably big? Opinions differ, but the default assumption seems to be that you generally would like to see all your expected frequencies larger than about 5, though for larger tables, you would probably be okay if at least 80% of the expected frequencies are above 5 and none of them are below 1. However, these seem to have been proposed as rough guidelines, not hard and fast rules; and they seem somewhat conservative (Larntz, 1978).
- Data are independent of one another. One somewhat hidden assumption of the chi-square test is that you have to believe that the observations are genuinely independent. Suppose we are interested in the proportion of babies born at a particular hospital that are boys. We walk around the maternity wards and observe 20 girls and only 10 boys. Seems like a pretty convincing difference, right? But later on, it turns out that we’d actually walked into the same ward 10 times, and in fact, we’d only seen 2 girls and 1 boy. Not as convincing, is it? Our original 30 observations were massively non-independent. And were only, in fact, equivalent to 3 independent observations. Obviously, this is an extreme(ly silly) example, but it illustrates the fundamental issue. Non-independence “stuffs things up”. Sometimes it causes you to falsely reject the null, as the silly hospital example illustrates, but it can go the other way too. Let’s consider what would happen if we’d done the cards experiment slightly differently: instead of asking 200 people to try to imagine sampling one card at random, suppose we asked 50 people to select 4 cards. One possibility would be that everyone selects one heart, one club, one diamond and one spade (in keeping with the “representativeness heuristic”; Tversky & Kahneman 1974). This is highly non-random behaviour from people, but in this case, we would get an observed frequency of 50 for all four suits. For this example, the fact that the observations are non-independent (because the four cards that you pick will be related to each other) actually leads to the opposite effect, falsely retaining the null.
If you find yourself in a situation where independence is violated, it may be possible to use the McNemar test. Similarly, if your expected cell counts are too small, check out the Fisher exact test.
10.6 The Fisher exact test
What should you do if your cell counts are too small, but you’d still like to test the null hypothesis that the two variables are independent? One answer would be “collect more data”, but that’s far too glib: there are a lot of situations in which it would be either infeasible or unethical to do. If so, statisticians are morally obligated to provide scientists with better tests. In this instance, Fisher (1922) kindly provided the right answer to the question. To illustrate the basic idea, let’s suppose we’re analysing data from a field experiment, looking at the emotional status of people accused of witchcraft. Some of them are currently being burned at the stake.47 Unfortunately for the scientist (but rather fortunately for the general populace), it’s quite hard to find people in the process of being set on fire, so the cell counts are microscopic. The salem.csv file illustrates the point.
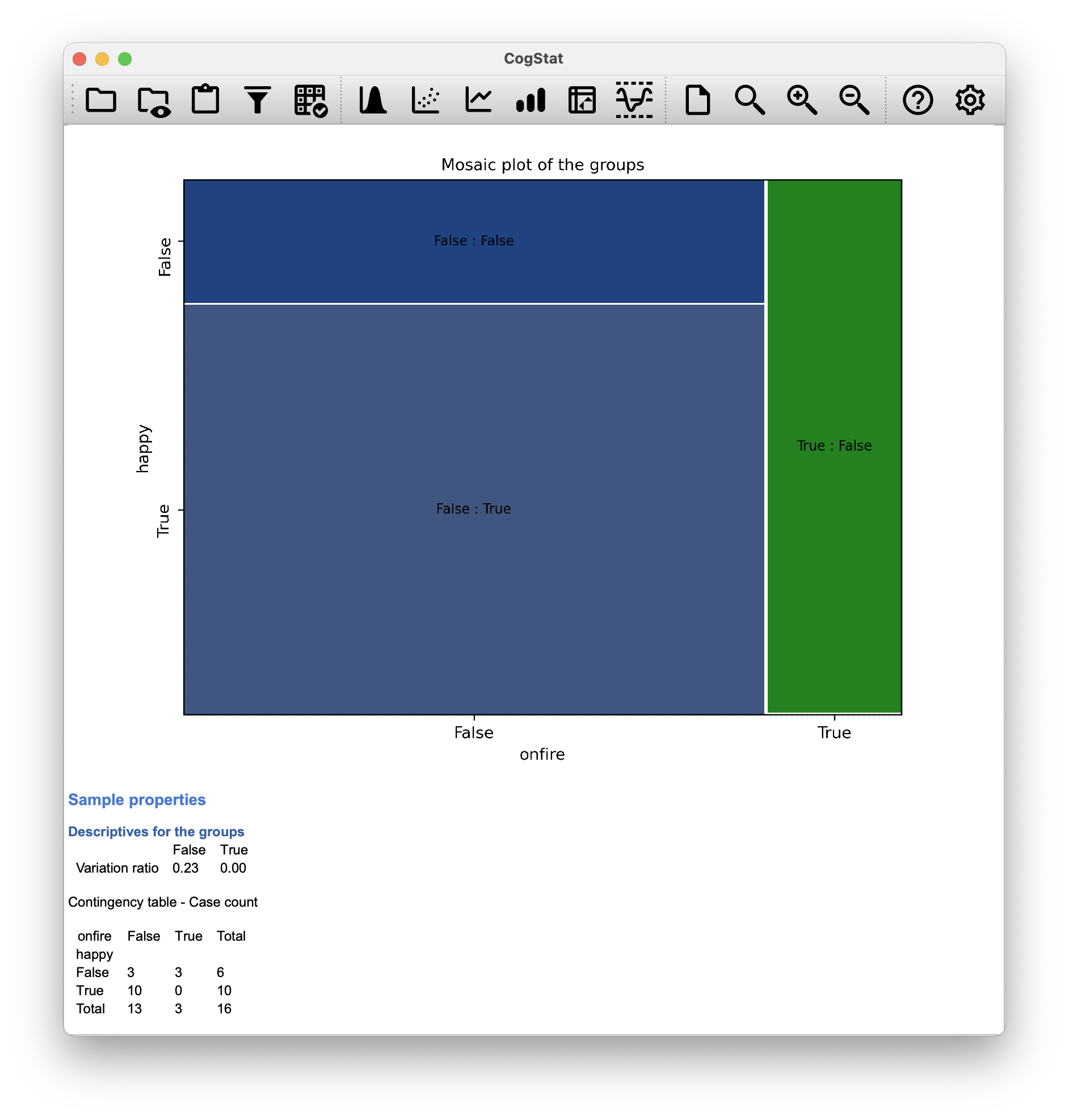
Figure 10.10: The salem data set
Looking at this data, you’d be hard pressed not to suspect that people not on fire are more likely to be happy than people on fire. However, the chi-square test (even with the Yates correction for the 2x2 data) makes this very hard to test because of the small sample size.

We’d really like to be able to get a better answer than this provided we really don’t want to be on fire. This is where Fisher’s exact test (Fisher, 1922a) comes in very handy. The Fisher exact test works somewhat differently to the chi-square test (or in fact any of the other hypothesis tests in this book) insofar as it doesn’t have a test statistic; it calculates the -value “directly”.
Let’s have some notation:
| Happy | Sad | Total | |
|---|---|---|---|
| Set on fire | |||
| Not set on fire | |||
| Total |
In order to construct the test Fisher treats both the row and column totals (, , and ) are known, fixed quantities; and then calculates the probability that we would have obtained the observed frequencies that we did (, , and ) given those totals. In the notation that we developed in Chapter 7 this is written: and as you might imagine, it’s a slightly tricky exercise to figure out what this probability is, but it turns out that this probability is described by a distribution known as the hypergeometric distribution. Now that we know this, what we have to do to calculate our -value is calculate the probability of observing this particular table or a table that is “more extreme”.48 Back in the 1920s, computing this sum was daunting even in the simplest of situations, but these days it’s pretty easy as long as the tables aren’t too big and the sample size isn’t too large. The conceptually tricky issue is to figure out what it means to say that one contingency table is more “extreme” than another. The easiest solution is to say that the table with the lowest probability is the most extreme. This then gives us the -value of .
The implementation of the test in CogStat is not yet available. The main thing we’re interested in here is the -value, which in this case is small enough () to justify rejecting the null hypothesis that people on fire are just as happy as people not on fire.
10.7 The McNemar test
Suppose you’ve been hired to work for the Australian Generic Political Party (AGPP), and part of your job is to find out how effective the AGPP political advertisements are. So, what you do, is you put together a sample of people and ask them to watch the AGPP ads. Before they see anything, you ask them if they intend to vote for the AGPP; after showing the ads, you ask them again to see if anyone has changed their minds. One way to describe your data is via the following contingency table:
| Before | After | Total | |
|---|---|---|---|
| Yes | 30 | 10 | 40 |
| No | 70 | 90 | 160 |
| Total | 100 | 100 | 200 |
At first pass, you might think that this situation lends itself to the Pearson test of independence (as per Chapter 10.2). However, we’ve got a problem: we have 100 participants but 200 observations. This is because each person has given us an answer in both the before and after columns. What this means is that the 200 observations aren’t independent of each other: if voter A says “yes” the first time and voter B says “no”, then you’d expect that voter A is more likely to say “yes” the second time than voter B! The consequence of this is that the usual test won’t give trustworthy answers due to the violation of the independence assumption. Now, if this were a really uncommon situation, I wouldn’t be bothering to waste your time talking about it. But it’s not uncommon at all: this is a standard repeated measures design, and none of the tests we’ve considered so far can handle it.
The solution to the problem was published by McNemar (1947). The trick is to start by tabulating your data in a slightly different way:
| Before: Yes | Before: No | Total | |
|---|---|---|---|
| After: Yes | 5 | 5 | 10 |
| After: No | 25 | 65 | 90 |
| Total | 30 | 70 | 100 |
This is exactly the same data, but it’s been rewritten so that each of our 100 participants appears in only one cell. Because we’ve written our data this way, the independence assumption is now satisfied, and this is a contingency table that we can use to construct an goodness of fit statistic. However, as we’ll see, we need to do it in a slightly nonstandard way. To see what’s going on, it helps to label the entries in our table a little differently:
| Before: Yes | Before: No | Total | |
|---|---|---|---|
| After: Yes | |||
| After: No | |||
| Total |
Next, let’s think about what our null hypothesis is: it’s that the “before” test and the “after” test have the same proportion of people saying, “Yes, I will vote for AGPP”. Because of the way we have rewritten the data, it means that we’re now testing the hypothesis that the row totals and column totals come from the same distribution. Thus, the null hypothesis in McNemar’s test is that we have “marginal homogeneity”. That is, the row totals and column totals have the same distribution: , and similarly that . Notice that this means that the null hypothesis actually simplifies to .
In other words, as far as the McNemar test is concerned, it’s only the off-diagonal entries in this table (i.e. and ) that matter! After noticing this, the McNemar test of marginal homogeneity is no different to a usual test. After (automatically) applying the Yates correction, our test statistic becomes: or, to revert to the notation that we used earlier in this chapter: and this statistic has an (approximately) distribution with . However, remember that – just like the other tests – it’s only an approximation, so you need to have reasonably large expected cell counts for it to work.
Now that you know what the McNemar test is all about, lets actually run one. The agpp.csv file contains the raw data. It contains three variables, an id variable that labels each participant in the data set, a responseBefore variable that records the person’s answer when they were asked the question the first time, and a responseAfter variable that shows the answer that they gave when asked the same question a second time.
Let us think what we want to do here. We have the same participants giving us two answers. We want to test whether the two answers (the before and the after) are independent of each other. Or, in other words, we want to compare a reapeated measure. In CogStat, we need to select Compare repeated measures variables and add the responseBefore and responseAfter variables to the Selected variables box to run an analysis (Figure 10.11). The results are shown in Figure 10.12.
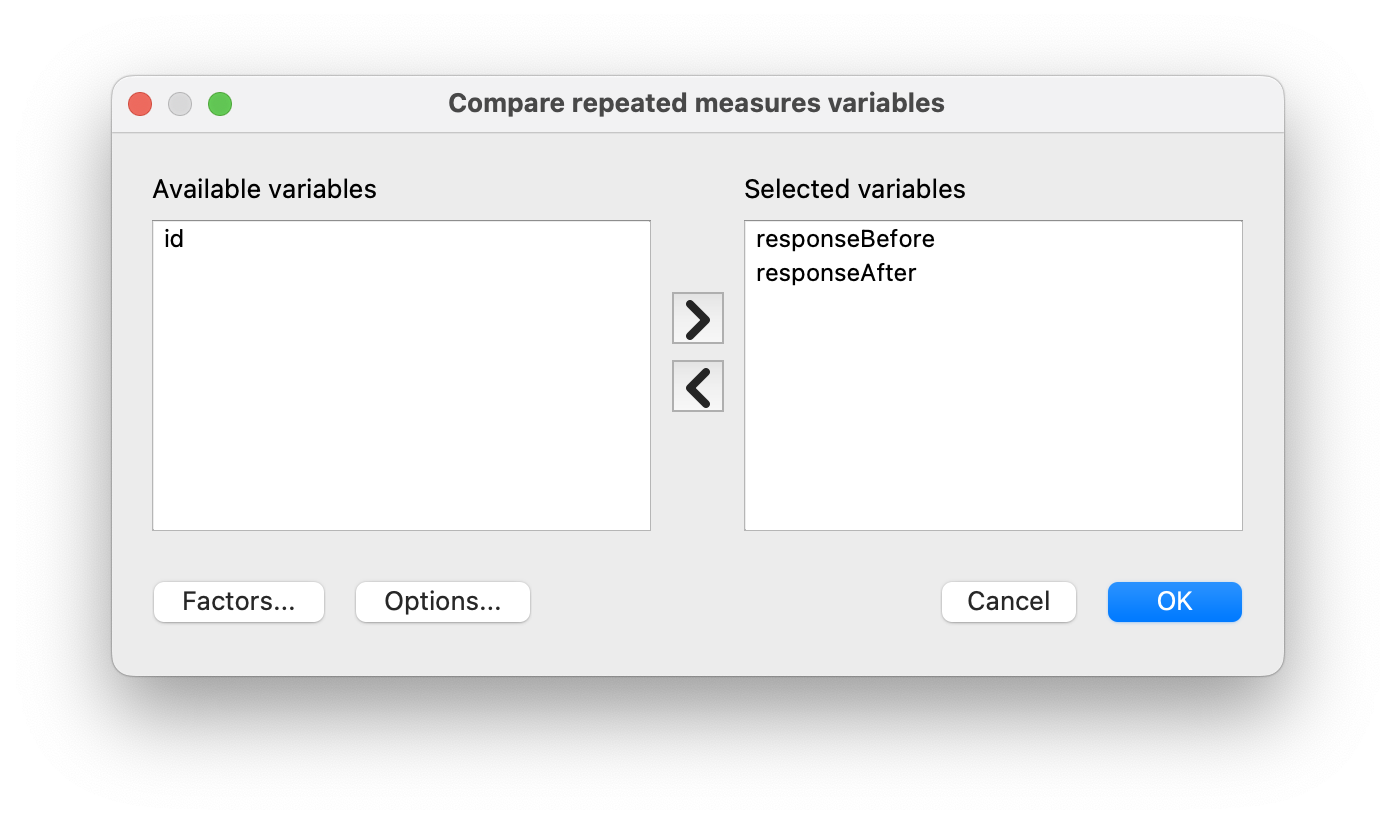
Figure 10.11: Repeated measures analysis of the AGPP data in CogStat.
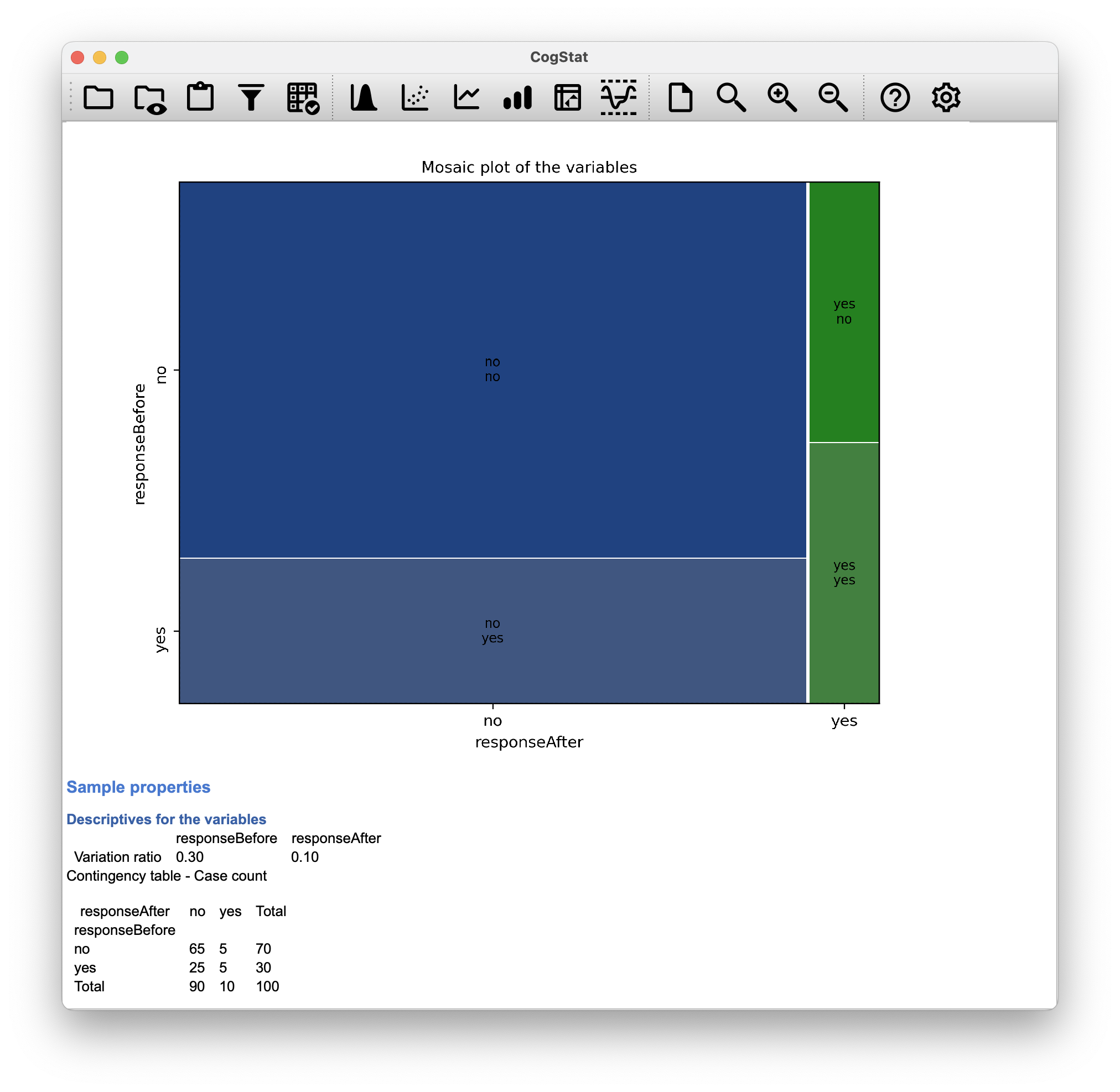
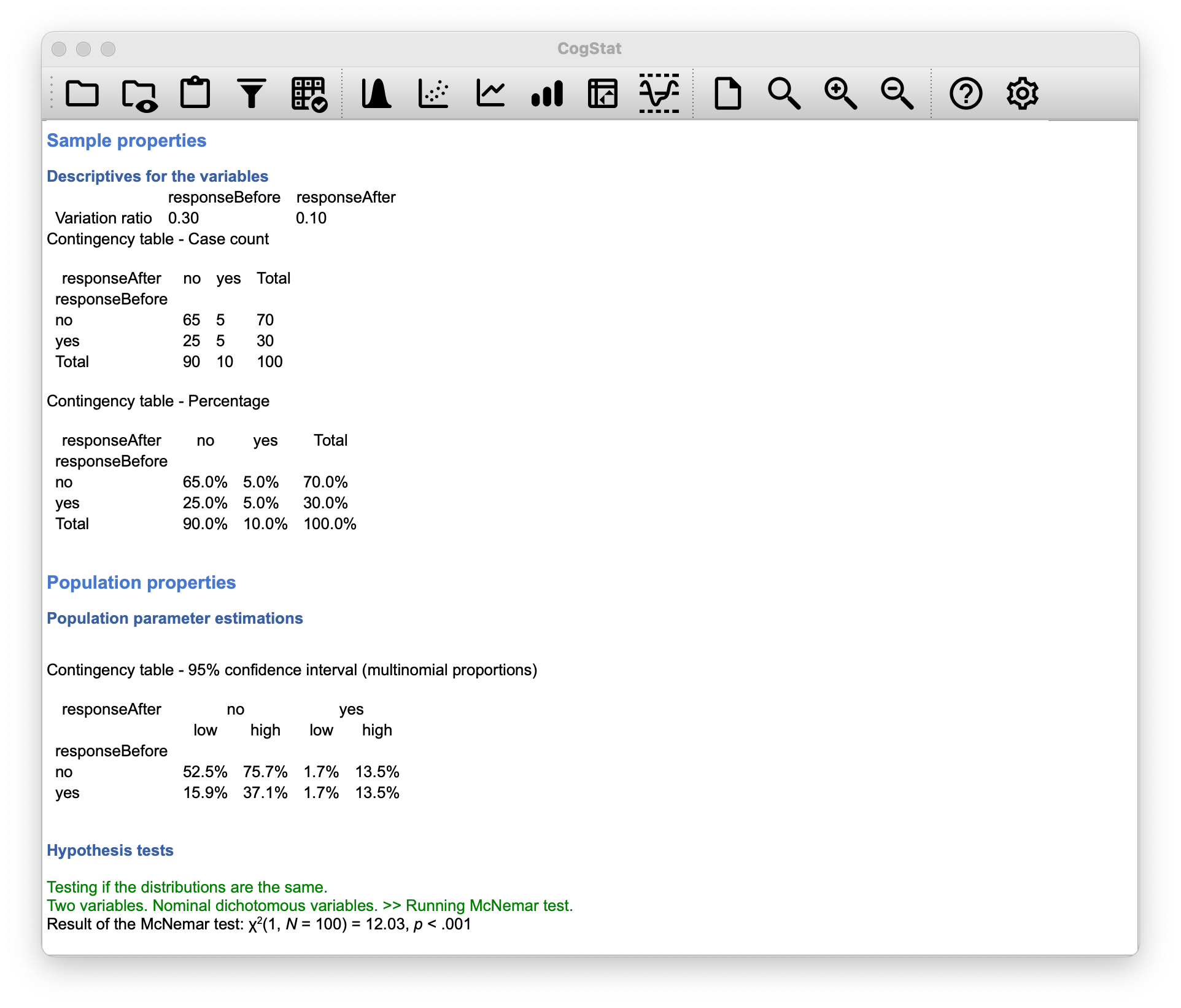
Figure 10.12: Results of the repeated measures analysis of the AGPP data in CogStat.
Hypothesis tests
Testing if the distributions are the same.
Two variables. Nominal dichotomous variables. >> Running McNemar test.
Result of the McNemar test: χ2(1, N = 100) = 12.03, p < .001
And we’re done. We’ve just run a McNemar’s test automatically, since our data set was identified by CogStat as categorical data.
The results would tell us something like this:
The test was significant (), suggesting that people were not just as likely to vote AGPP after the ads as they were before hand. In fact, the ads had a negative effect: people were less likely to vote AGPP after seeing the ads.
10.8 What’s the difference between McNemar and independence?
Let’s go back to the beginning of the chapter and look at the cards data set again. If you recall, the experimental design described involved people making two choices. Because we have information about the first choice and the second choice that everyone made, we can construct the following contingency table that cross-tabulates the first choice against the second choice.
| clubs | diamonds | hearts | spades | Total | |
| clubs | 10 | 9 | 10 | 6 | 35 |
| diamonds | 20 | 4 | 13 | 14 | 51 |
| hearts | 20 | 18 | 3 | 23 | 64 |
| spades | 18 | 13 | 15 | 4 | 50 |
| Total | 68 | 44 | 41 | 47 | 200 |
First, we wanted to know whether the choice you make the second time is dependent on the choice you made the first time (for this, we’ll run the Explore relation of variable pair analysis). This is where a test of independence is useful, and what we’re trying to do is see if there’s some relationship between the rows and columns of this table.
Second, we wanted to know if on average, the frequencies of suit choices were different the second time than the first time. In that situation, we’re trying to see if the row totals in cardChoices (i.e. the frequencies for choice_1) are different from the column totals (i.e. the frequencies for choice_2). That’s when we’d use the McNemar test. However, when running the Compare repeated measures variables analysis, we get an error, as the function for non-dichotomous nominal data is not implemented yet.
Here’s the result if we run the Explore relation of variable pair analysis in CogStat:
Hypothesis tests
Testing if variables are independent.
Nominal variables. >> Running Cramér's V.
Sensitivity power analysis. Minimal effect size to reach 95% power with the present sample size for the present hypothesis test. Minimal effect size in w: 0.34.
Result of the Pearson's chi-squared test: χ2(9, N = 200) = 29.24, p < .001
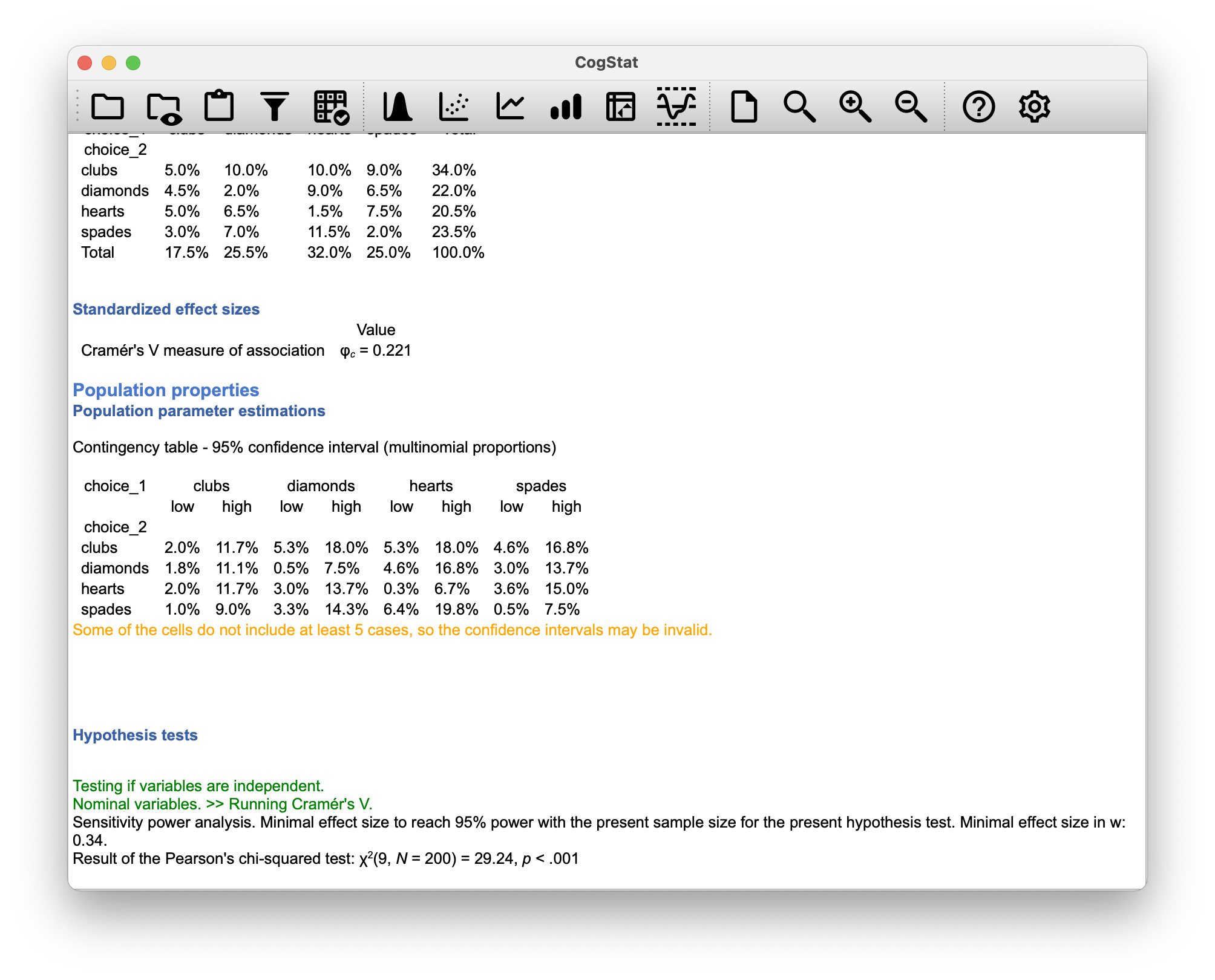
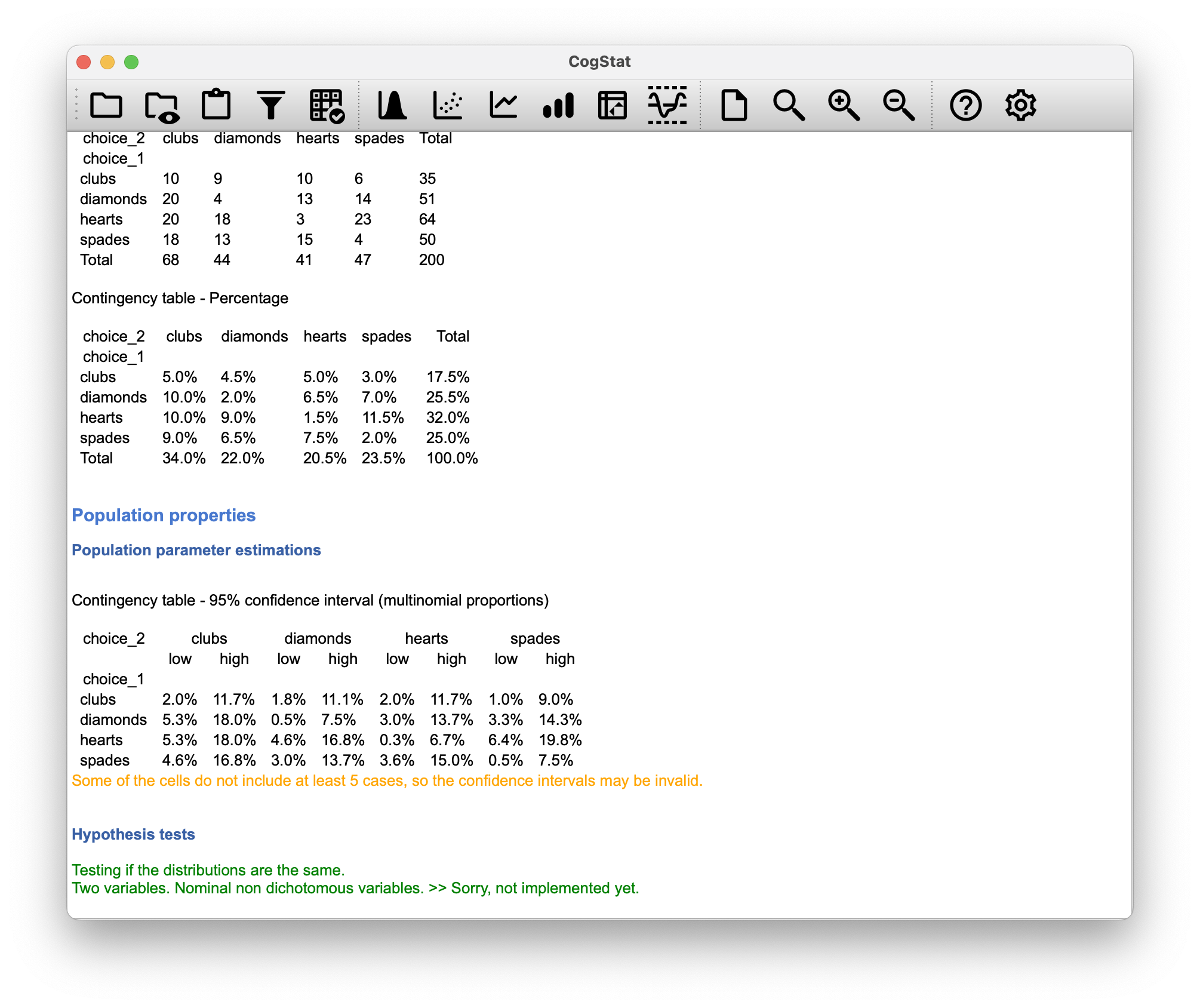
Figure 10.13: Hypothesis test results when running either Compare repeated measures variables or Explore relation of variable pair in CogStat.
For the second case, running the McNemar test, the answer would be McNemar’s chi-squared = , df = , p-value = . This is a significant result, suggesting that the frequencies of suit choices were different the second time than the first time.
Notice that the results are different! These aren’t the same test.
10.9 Summary
The key ideas discussed in this chapter are:
- The chi-square goodness of fit test (Section 10.1) is used when you have a table of observed frequencies of different categories; the null hypothesis gives you a set of “known” probabilities to compare them to.
- The chi-square test of independence (Section 10.2) is used when you have a contingency table (cross-tabulation) of two categorical variables. The null hypothesis is that there is no relationship/association between the variables.
- Effect size for a contingency table can be measured in several ways (Section 10.4). In particular, we noted the Cramér’s statistic.
- Both versions of the Pearson test rely on two assumptions: that the expected frequencies are sufficiently large and that the observations are independent (Section 10.5). The Fisher exact test (Section 10.6) can be used when the expected frequencies are small. The McNemar test (Section 10.7) can be used for some kinds of violations of independence.
If you’re interested in learning more about categorical data analysis, an excellent first choice would be Agresti (1996), which, as the title suggests, provides an Introduction to Categorical Data Analysis. If the introductory book isn’t enough for you (or you can’t solve the problem you’re working on), you could consider Agresti (2002), Categorical Data Analysis. The latter is a more advanced text, so it’s probably not wise to jump straight from this book to that one.
References
This, again, is an over-simplification. It works nicely for quite a few situations, but every now and then, we’ll come across degrees of freedom values that aren’t whole numbers. Don’t let this worry you too much – when you come across this, just remind yourself that “degrees of freedom” is actually a bit of a messy concept. For an introductory class, it’s usually best to stick to the simple story.↩︎
In practice, the sample size isn’t always fixed… e.g. we might run the experiment over a fixed period of time, and the number of people participating depends on how many people show up. That doesn’t matter for the current purposes.↩︎
To some people, this advice might sound odd or at least in conflict with the “usual” advice on how to write a technical report. Students are typically told that the “results” section of a report is for describing the data and reporting statistical analysis, and the “discussion” section provides interpretation. That’s true as far as it goes, but people often interpret it way too literally. Provide a quick and simple interpretation of the data in the results section so that the reader understands what the data are telling us. Then, in the discussion, try to tell a bigger story; about how my results fit the rest of the scientific literature. In short, don’t let the “interpretation goes in the discussion” advice turn your results section into incomprehensible garbage. Being understood by your reader is much more important.↩︎
Complicating matters, the -test is a special case of a whole class of tests that are known as likelihood ratio tests.↩︎
Technically, here is an estimate, so we should probably write it .↩︎
A problem many of us worry about in real life.↩︎
Technically, CogStat uses
chi2_contingencyfunction fromscipywithout specifying thecorrectionparameter which defaults totrue.↩︎This example is based on a joke article published in the Journal of Irreproducible Results.↩︎
Not surprisingly, the Fisher exact test is motivated by Fisher’s interpretation of a -value, not Neyman’s!↩︎